近三十年來各種類型的鋼結構在我國獲得了大范圍的應用,其快速發展促進了對它們設計方法的研究。由于研究手段的現代化,鋼結構穩定理論、抗震設計理論和組合結構理論都取得了巨大的進展,鋼結構及其配套新技術也不斷出現。雖然鋼結構應用廣泛,鋼結構設計規范也已經進入第 4 個版本即 2017 版本,但是鋼結構設計仍存在很多亟待改進的地方,例如外露式柱腳的錨栓能否參與抗剪以及抗剪承載力如何計算,外包式柱腳的外包混凝土層是鋼柱的支座還是與鋼柱共同工作形成了鋼骨混凝土(SRC)柱,抗震結構的梁柱節點域應設計成強節點域還是弱節點域,等等。浙江大學童根樹教授在參與鋼結構相關規范的過程中對這些問題進行了一些思考,并帶領團隊進行了相關深入研究,在重視理論的同時也偏向工程應用,積累了很多很好的設計經驗。為進一步促進和推動我國鋼結構設計方法和技術的發展,《鋼結構(中英文)》編輯部特邀童根樹教授將其在鋼結構設計研究中的新觀點、新方法和新結果進行系列介紹,以饗讀者,并歡迎大家交流和探討。

摘 要

采用薄壁構件理論對 C 形截面和 Z 形截面檁條在風吸力作用下的平衡微分方程進行了理論推導和有限元驗證。結果表明:Z 形檁條求解扭轉變形的平衡微分方程中,扭矩項很小,從而推論出 Z 形截面檁條在風吸力下產生的扭轉變形很小;薄壁構件的理論結果與有限元分析結果吻合;Z 形檁條的承載力高于同一規格的 C 形檁條,應優先采用 Z 形截面。

1 問題的引出

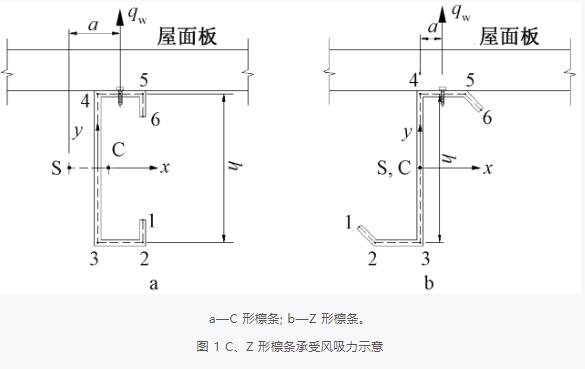
圖 1 分別為 C 形檁條和 Z 形檁條承受風吸力示意。當截面高、寬、厚度相同的情況下,假設都為簡支檁條時,是采用 C 形還是 Z 形截面,薄壁構件理論分析將給我們提供答案。

2 C 形檁條

考慮側向彎曲和扭轉,C 形檁條的線性分析總勢能為:

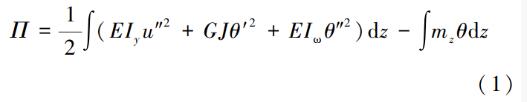
式中: I_y、J、I_ω 分別為 C 形截面繞 y 軸的慣性矩、自由扭轉常數和翹曲慣性矩; E、G 分別為鋼材彈性模量和剪切模量; u、θ 分別為截面在 x 方向的位移和繞剪切中心的扭轉角; m_z 為單位長度上的扭矩,計算式為:

式中: q_w 為風吸力; a 為自攻螺釘到剪切中心的距離,見圖 1。

因為屋面采用了滿鋪的壓型鋼板,檁條與壓型鋼板的連接采用了自攻螺釘,整個截面繞上翼緣轉動,剪切中心水平位移與截面的扭轉角存在如下的關系:

將式(3)代入式(1)得到:

其中

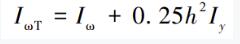
對式(4) 進行變分,分部積分后得到平衡微分方程:

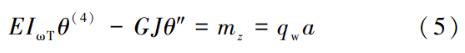
3 Z 形檁條

Z 形檁條如圖 1b 所示, x、y 是平行軸,不是形心主軸,須考慮雙向彎曲和扭轉,線性分析總勢能為:

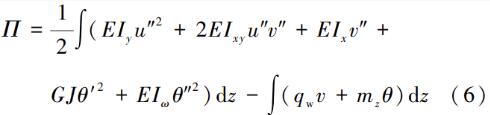
式中: I_x 、I_xy 分別為繞 x 軸的慣性矩和交叉積; v 為豎向位移,其他符號的意義同式(1)。

整個截面繞上翼緣轉動, 將式(3)代入式(6),得:

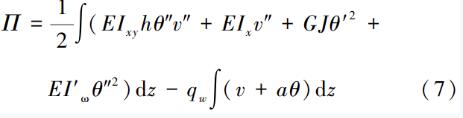
其中

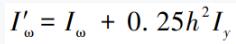
對式(7)變分并分部積分,得到平衡微分方程:

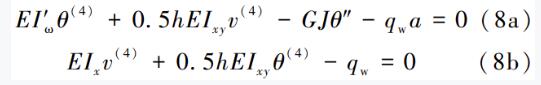
由式(8b)得:

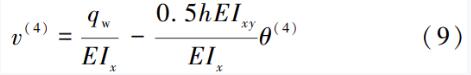
代入式(8a)得到 :

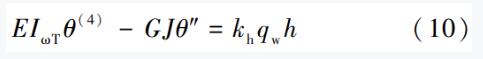
其中

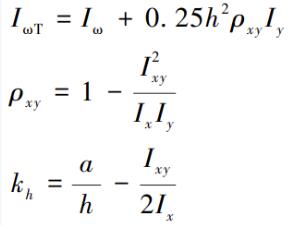
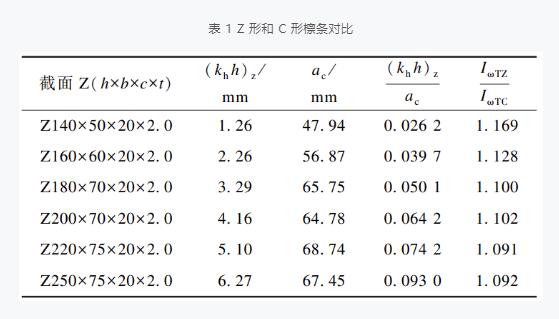
表 1 列 出 了 6 種 Z 形截面計算扭矩的力臂(k_h),還給出了同樣規格的 C 形截面按式(5)計算扭矩的 a 值,記為 a_c ,比值(k_hh)_z/a_c 代表了 Z 形檁條和 C 形檁條在相同風吸力下的扭矩比值,其值僅為 2.6% ~ 9.3%,表明 Z 形檁條的翹曲慣性矩略大于 C 形檁條,于是得到如下非常有意義的結論:Z 形截面在風吸力下幾乎不扭轉,所以應優先采用 Z 形截面,不管是檁條還是墻檁。

4 有限元分析對比

圖 1 中自由翼緣(受壓區)的 2 號點和 3 號點的應力對比如圖 2 和圖 3 所示。分析模型的跨度為5 m,每隔 250 mm 在上翼緣中點施加 500 N 風吸力,計算截面的 h = 140 ~ 250 mm, 厚度為 2.0, 2.2,2.5 mm,共 18 個截面。

圖 2 給出斜卷邊 Z 形截面的計算結果表明:1) 薄壁構件的理論結果與有限元分析結果很接近;2) 點 2 和點 3 的應力也比較接近,說明斜卷邊 Z 形檁條下翼緣的水平彎曲位移很小。

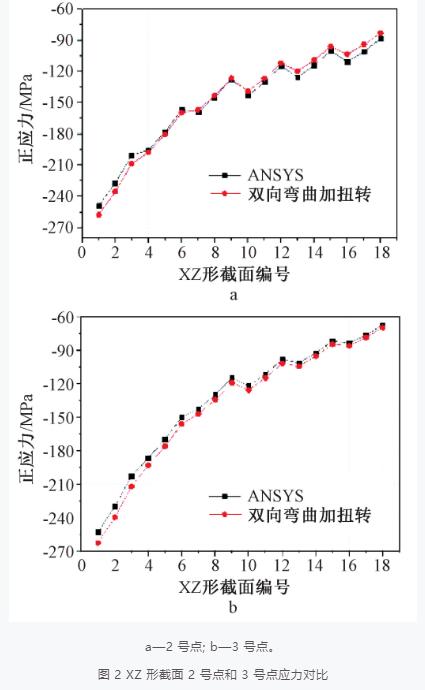
圖 3 給出了 C 形截面下翼緣的 2 號點和 3 號點的應力。可知:卷邊側的 2 號點為拉應力,腹板側的3 號點的壓應力很大,說明下翼緣產生了很大的水平彎曲,從而抵消了豎向彎曲在 2 號點產生的壓應力。

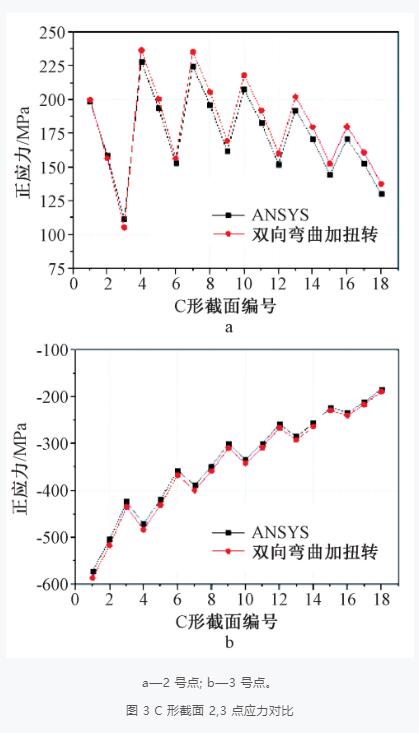
C 形截面 3 號點的壓應力是同規格的 Z 形截面下翼緣壓應力的 2.2 ~ 2.6 倍,這意味著 C 形檁條的承載力小于 Z 形截面的。

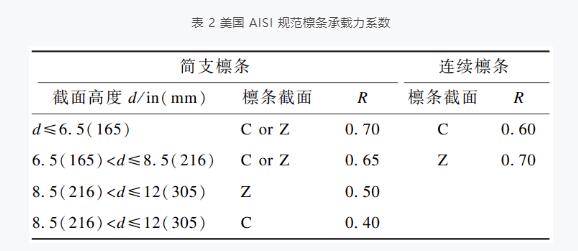
另外,美國鋼鐵學會 AISI 規范對 C 形截面和Z 截面的承載力計算公式中,Z 形截面的承載力系數 R 是高于 C 形截面的(表 2),從中也反映了上述規律。

5 結 論

C 形檁條在風吸力下會“放飛自我”,扭轉變形大,而目前的拉條布置對檁條提供的約束作用小,所以宜少用 C 形截面。建議在能夠采用 Z 形截面檁條的地方,應盡量采用 Z 形檁條和 Z 形墻檁。